Lecture 2: Optimization Problems | Lecture Videos | Introduction to Computational Thinking and Data Science | Electrical Enginee
Prof. Guttag explains dynamic programming and shows some applications of the process.
ocw.mit.edu
※위의 내용을 기반을로 함
Greedy 알고리즘의 장단점
- 적용 쉬움
- 효율적임
- 하지만 최적값을 만들지 못함
- 얼마나 좋은 값을 내보냈는지도 알 수 없음
Brute Force 알고리즘
- 가능한 모든 조합을 만들어냄
- 이 중 허용된 무게를 벗어난 값들을 제거함
- 남아있는 조합 중 가장 높은 가치를 가진것을 선택함
트리 탐색 적용
- 트리는 위에서 아래로 Root(뿌리)로 부터 시작함
- 남아있는 아이템중 첫번째 품목을 선택함
- 아직 가방에 장소가 남아있다면, 노드를 하나 생성하고 해당 품목을 선택한 결과를 그 노드의 왼쪽에 생성함
- 선택하지 않은 경우는 해당 노드의 오른쪽에 생성함
- 재귀적으로 적용함
- 마지막으로, 가장 높은 가치를 가지며 구속조건을 충족하는 값을 선택함
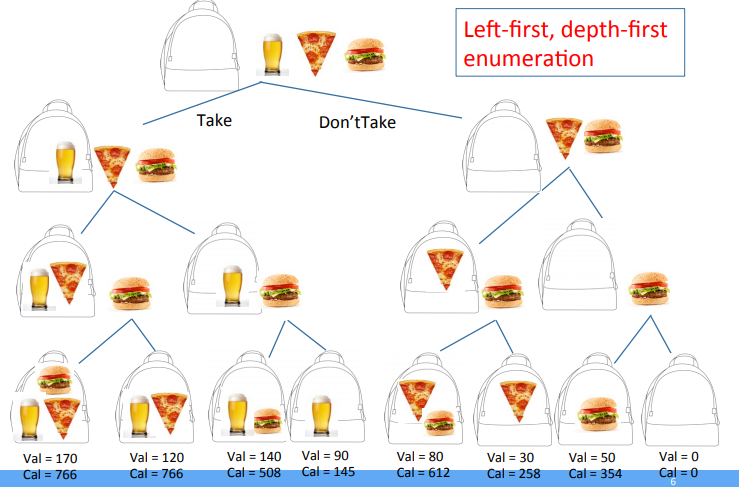

컴퓨테이션 복잡도
- 생성된 노드의 갯수에 근거함
- Level(Depth)는 선택해야 하는 품목들의 갯수
- Level i 에서 노드의 갯수는 2^i
- 노드의 갯수는
$1 + 2 + 4 + 8 + ... + 2^i$
\[ \sum_{i=0}^{n} 2^{i} = 2^{n+1} -1 \]
\[ O(2^n-1)\]
- 확실한 최적화 방법: 구속조건을 넘어서는 트리는 탐색하지 않음
- 복잡도는 그대로임
Decision Tree적용을 위한 Header
def maxVal (toConsider, avail):
"""toConsider는 물품들의 List,
avail은 무게
Return: 0/1 Knapsack problem이 해결됬을때의 전체 value와 품목들"""toConsider: Tree에서 아직 탐색되지 않은 부분
avail: 가용한 공간
maxVal 구성
def maxVal (toConsider, avail):
"""toConsider는 물품들의 List,
avail은 무게
Return: 0/1 Knapsack problem이 해결됬을때의 전체 value와 품목들"""
#Base case
if toConsider == [] or avail == 0:
result = (0,())
#첫번째 아이템의 cost(unit)이 현재 가용한 부분보다 양이 많은지 판별. 많다면 더이상 고려할 필요 없으니 스킵
#오른쪽 브렌치만
elif toConsider[0].getUnits() > avail:
result = maxVal(toConsider[1:], avail)
#양쪽 브렌치 고려
else:
#왼쪽브랜치
nextItem = toConsider[0]
# 아이템을 취하게되면 가용한 공간이 줄어들게됨
withVal, withToTake = maxVal(toConsider[1:], avail - nextItem.getUnits())
withVal += nextItem.getValue()
# 오른쪽 브렌치
withoutVal, withoutTOTake = maxVal(toConsider[1:], avail)
if withVal > withoutVal:
result = (withVal,withToTake + (nextItem,))
else:
result = (withoutVal, withoutToTake)
return result
테스트하기
def testMaxVal(foods, maxUnits, printItems = True):
print('Use search tree to allocate', maxUnits,
'calories')
val, taken = maxVal(foods, maxUnits)
print('Total value of items taken =', val)
if printItems:
for item in taken:
print(' ', item)
테스트용 전체 코드
def maxVal(toConsider, avail):
"""Assumes toConsider a list of items, avail a weight
Returns a tuple of the total value of a solution to the
0/1 knapsack problem and the items of that solution"""
if toConsider == [] or avail == 0:
result = (0, ())
elif toConsider[0].getCost() > avail:
#Explore right branch only
result = maxVal(toConsider[1:], avail)
else:
nextItem = toConsider[0]
#Explore left branch
withVal, withToTake = maxVal(toConsider[1:],
avail - nextItem.getCost())
withVal += nextItem.getValue()
#Explore right branch
withoutVal, withoutToTake = maxVal(toConsider[1:], avail)
#Choose better branch
if withVal > withoutVal:
result = (withVal, withToTake + (nextItem,))
else:
result = (withoutVal, withoutToTake)
return result
def testMaxVal(foods, maxUnits, printItems = True):
print('Use search tree to allocate', maxUnits,
'calories')
val, taken = maxVal(foods, maxUnits)
print('Total value of items taken =', val)
if printItems:
for item in taken:
print(' ', item)
names = ['wine', 'beer', 'pizza', 'burger', 'fries',
'cola', 'apple', 'donut', 'cake']
values = [89,90,95,100,90,79,50,10]
calories = [123,154,258,354,365,150,95,195]
foods = buildMenu(names, values, calories)
testGreedys(foods, 750)
print('')
testMaxVal(foods, 750)
결과값
Use greedy by value to allocate 750 calories
Total value of items taken = 284.0
burger: <100, 354>
pizza: <95, 258>
wine: <89, 123>
Use greedy by cost to allocate 750 calories
Total value of items taken = 318.0
apple: <50, 95>
wine: <89, 123>
cola: <79, 150>
beer: <90, 154>
donut: <10, 195>
Use greedy by density to allocate 750 calories
Total value of items taken = 318.0
wine: <89, 123>
beer: <90, 154>
cola: <79, 150>
apple: <50, 95>
donut: <10, 195>
Use search tree to allocate 750 calories
Total value of items taken = 353
cola: <79, 150>
pizza: <95, 258>
beer: <90, 154>
wine: <89, 123>Greedy Algorithm은 지난번에 사용된 것과 동일함
Value가 353으로 높아진것을 볼 수 있음.
Search Tree가 잘 작동했음
- 더 나은 값을 내보냄
- 더 빠르게 내보냄
- 하지만 2^8은 그렇게 큰 숫자가 아님
더 큰 숫자로 테스트
import random
def buildLargeMenu(numItems, maxVal, maxCost):
items = []
for i in range(numItems):
items.append(Food(str(i),
random.randint(1, maxVal),
random.randint(1, maxCost)))
return itemsRandom을 Import함.
원하는 숫자만큼 Loop를 돌려 메뉴를 만들 수 있도록 설정
import random
def buildLargeMenu(numItems, maxVal, maxCost):
items = []
for i in range(numItems):
items.append(Food(str(i),
random.randint(1, maxVal),
random.randint(1, maxCost)))
return items
for numItems in (5, 10, 15, 20, 25, 30, 35, 40, 45):
print('Try a menu with', numItems, 'items')
items = buildLargeMenu(numItems, 90, 250)
testMaxVal(items, 750, False)
결과
Try a menu with 5 items
Use search tree to allocate 750 calories
Total value of items taken = 129
Try a menu with 10 items
Use search tree to allocate 750 calories
Total value of items taken = 384
Try a menu with 15 items
Use search tree to allocate 750 calories
Total value of items taken = 531
Try a menu with 20 items
Use search tree to allocate 750 calories
Total value of items taken = 563
Try a menu with 25 items
Use search tree to allocate 750 calories
Total value of items taken = 715
Try a menu with 30 items
Use search tree to allocate 750 calories
Total value of items taken = 691
Try a menu with 35 items
Use search tree to allocate 750 calories
Total value of items taken = 627
Try a menu with 40 items
Use search tree to allocate 750 calories
Total value of items taken = 786
Try a menu with 45 items
Use search tree to allocate 750 calories시간이 급격히 오래걸림
해결방안
- 이론적으론 해결 불가
- 실무적으론 해결 가능
- Dynamic Programming

Dynamic Programming 이란(동적 프로그래밍)?
- 가끔 이름은 그냥 이름일 뿐
“The 1950s were not good years for mathematical research…I felt I had to do something to shield Wilson and the Air Force from the fact that I was really doing mathemaics...What title, what name, could I choose?... It's impossible to use the word dynamic in a pejorative sense. Try thinking of some combination that will possibly give it a pejorative meaning. It's impossible. Thus, I thought dynamic programming was a good name. It was something not even a Congressman could object to. So I used it as an umbrella for my activities -- Richard Bellman
- 국방부로 부터 후원 받던 시절, 국방부는 수학이 들어가는 말을 원치 않았음
- 그래서 그냥 아무 의미없는 단어를 하나 고
르기로 함
피보나치 수열 표현
def fib(n):
if n == 0 or n == 1:
return 1
else:
return fib(n - 1) + fib(n - 2)
fib(120) = 8,670,007,398,507,948,658,051,921
테스트코드
for i in range(121):
print('fib(' + str(i) + ') =', fib(i))fib(0) = 1
fib(1) = 1
fib(2) = 2
fib(3) = 3
fib(4) = 5
fib(5) = 8
fib(6) = 13
fib(7) = 21
fib(8) = 34
fib(9) = 55
fib(10) = 89
fib(11) = 144
fib(12) = 233
fib(13) = 377
fib(14) = 610
fib(15) = 987
fib(16) = 1597
fib(17) = 2584
fib(18) = 4181
fib(19) = 6765
fib(20) = 10946
fib(21) = 17711
fib(22) = 28657
fib(23) = 46368
fib(24) = 75025
fib(25) = 121393
fib(26) = 196418
fib(27) = 317811
fib(28) = 514229
fib(29) = 832040
fib(30) = 1346269
fib(31) = 2178309
fib(32) = 3524578
fib(33) = 5702887
fib(34) = 9227465
fib(35) = 14930352
fib(36) = 24157817
fib(37) = 39088169- 37부터 급격히 느려져서 중단함
피보나치 수열이 느린 이유
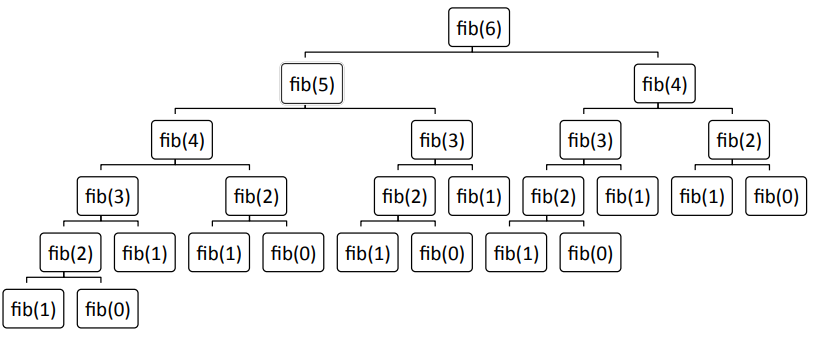
- 왼쪽 아래에서부터 계산해 가면서 위로 올라옴
- 계산 과정 중 중복되는 값을 볼 수 있음
- 중복되는 값을 다시 계산하기 때문에 느릴 수 밖에 없음
- 만약 앞에서 계산한 값을 메모 할 수 있다면 더 빨라질 것임 (memoization)
피보나치 수열에 메모 이용
def fastFib(n, memo = {}):
""" n은 정수 이며 0보다 큰것으로 가정.
memo 는 n에 대한 피보나치 수열을 저장"""
if n == 0 or n ==1:
return 1
#memo dictionary안에 fib(n)값이 존재 하는지 확인한다
try:
return memo[n]
# Dictionary에 없다면 keyError가 생김. try excepttion에 대한 부분은 6-0001수업 참조
except KeyError:
result = fastFib(n-1, memo) + \
fastFib(n-2, memo)
memo[n] = result
return result테스트용 코드
for i in range(121):
print('fib(' + str(i) + ') =', fastFib(i))
결과
...
fib(110) = 70492524767089125814114
fib(111) = 114059301025943970552219
fib(112) = 184551825793033096366333
fib(113) = 298611126818977066918552
fib(114) = 483162952612010163284885
fib(115) = 781774079430987230203437
fib(116) = 1264937032042997393488322
fib(117) = 2046711111473984623691759
fib(118) = 3311648143516982017180081
fib(119) = 5358359254990966640871840
fib(120) = 8670007398507948658051921- 매우 빠르게 생성됨
- Dictionary의 'in' 기능은 O(1) 속도로 작동함. Hashable하기 때문에
- memory complexity는 O(n)일 듯
Memoizatino이 적용 가능할 때는?
- Optimal substructure: 전역 최적값이 로컬 최적값의 조합으로 표현 가능할때
fib(x) = fib(x-1) + fib(x-2)
- 하위 문제들이 오버랩 될때: 같은 문제를 여러번 해결해야 할때
fib(x)를 여러번 계산
0/1 Knapsack에도 적용 가능한가?
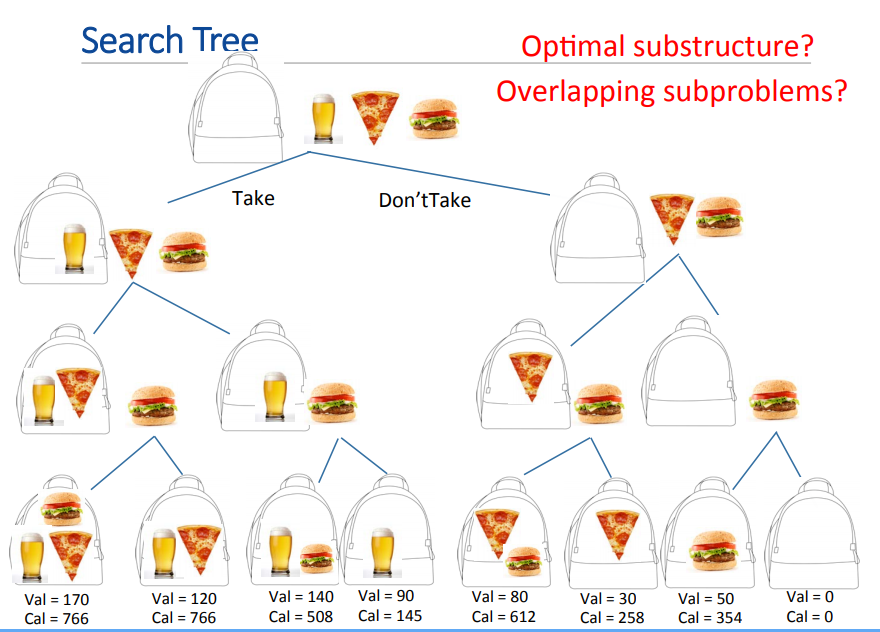
- Optimal Substructure 존재. 왼쪽과 오른쪽 중 적합한 값을 고르는 것이니까
- Overlap은 없음.
- 따라서 Speedup은 안됨
이 경우엔?
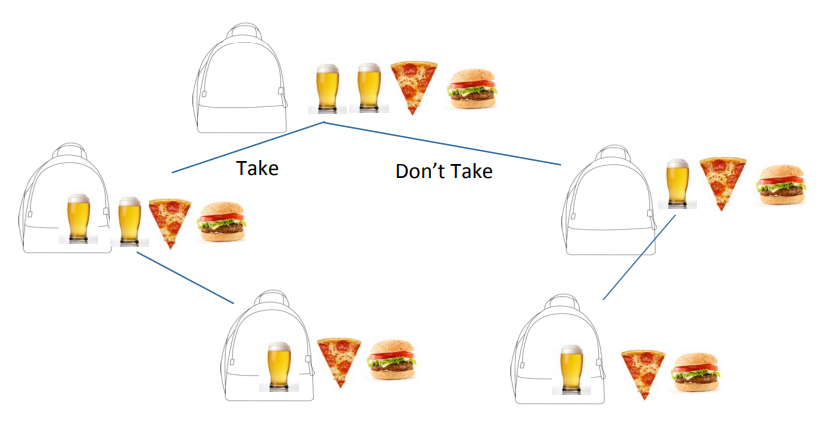
정답은
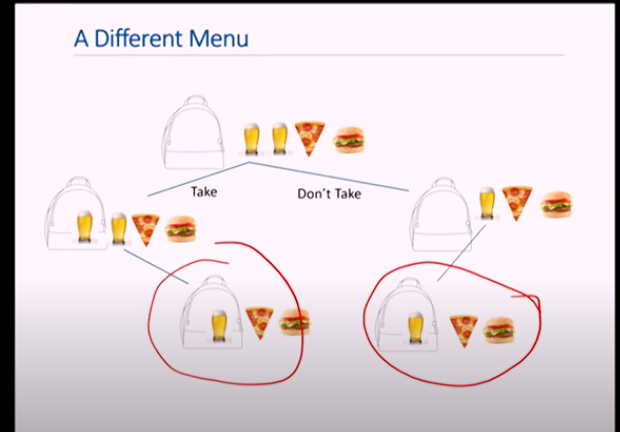
존재함
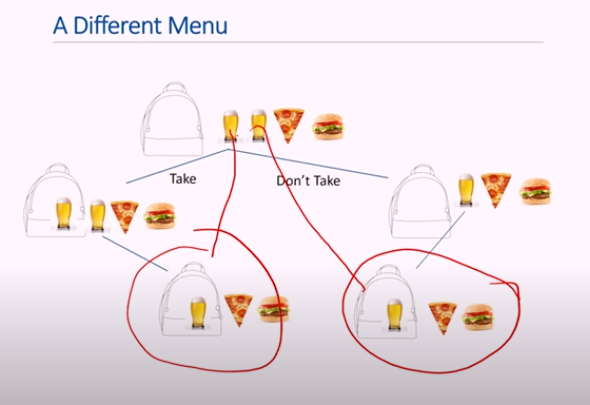
Search Tree
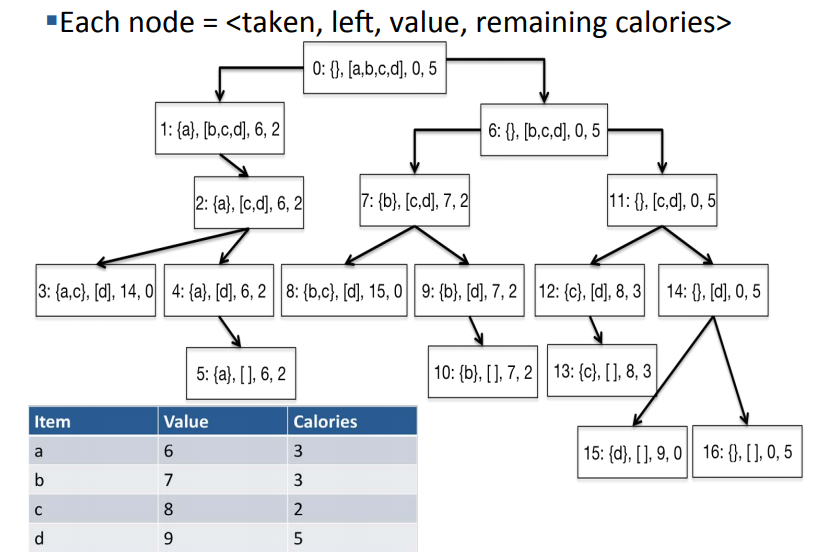
Knapsack 문제의 Dynamic programming을 해결할 tree임
- 중복되는 것 있음
- 각 노드에 쓰인 값은 index: 집은 물건, 남은 물건, 가치, 남은 칼로리 순서임
문제해결시 고려해야할 사항
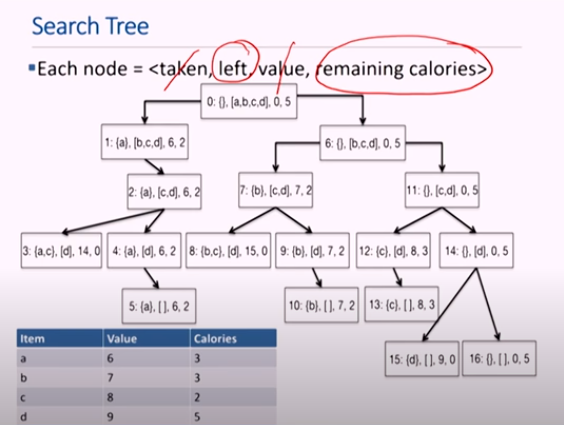
어떤 물건을 집었는지, 현재까지 가치가 얼마인지 신경 안씀. -> 남은 물건들과 남은 칼로리(공간)만 신경씀
- 남아있는 것들의 value를 최대화 하는것만 신경씀??
- 신경쓸것은 칼로리뿐
- 따라서 같은 숫자의 남은 칼로리가 있는 조합만 신경쓴다
- 남은 물건들로 부터 value최대화만이 관심있는 문제
중복되는 문제
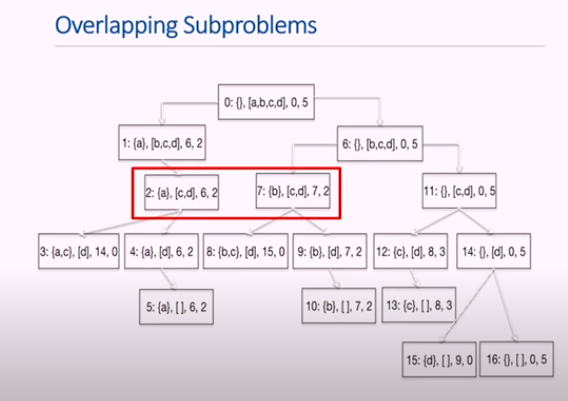
-남은 칼로리와, 남아있는 아이템의 종류가 같으니 둘은 같은 문제이다.
def fastMaxVal(toConsider, avail, memo = {}):
"""Assumes toConsider a list of subjects, avail a weight
memo supplied by recursive calls
Returns a tuple of the total value of a solution to the
0/1 knapsack problem and the subjects of that solution"""
if (len(toConsider), avail) in memo:
result = memo[(len(toConsider), avail)]
elif toConsider == [] or avail == 0:
result = (0, ())
elif toConsider[0].getCost() > avail:
#Explore right branch only
result = fastMaxVal(toConsider[1:], avail, memo)
else:
nextItem = toConsider[0]
#Explore left branch
withVal, withToTake =\
fastMaxVal(toConsider[1:],
avail - nextItem.getCost(), memo)
withVal += nextItem.getValue()
#Explore right branch
withoutVal, withoutToTake = fastMaxVal(toConsider[1:],
avail, memo)
#Choose better branch
if withVal > withoutVal:
result = (withVal, withToTake + (nextItem,))
else:
result = (withoutVal, withoutToTake)
memo[(len(toConsider), avail)] = result
return result- 알아서 돌려볼것
퍼포먼스 요약
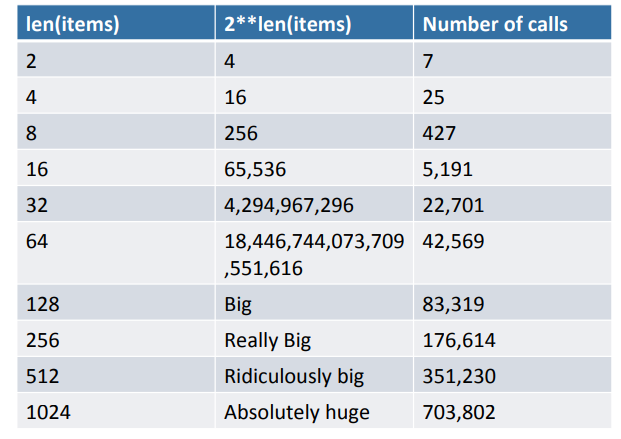
요약
- 퍼포먼스는 unique value의 갯수에 달려 있음
- Exponential한 문제도 풀 수 있음
'아카이브 > Computation + Python' 카테고리의 다른 글
| [Computation / Python] Knapsack Problems / Greedy Algorithm(최적화, Optimization) (0) | 2021.05.10 |
|---|
