[그래프 데이터베이스][무작정해보기] [6/30] A*(A-star) Algorithm 그림으로 이해하기.

다음 예제는 A*(A-Star) Algorithm 을 사용합니다. 그 전에 A* 알고리즘이 무엇인지 간단한 그림을 통해 이해해보도록 하겠습니다.

A* 알고리즘은 무엇이고 어디에 쓰이는가?

A*(pronounced "A-star") is a  graph traversal and  path search algorithm, which is often used in many fields of computer science due to its completeness, optimality, and optimal efficiency.
A*("에이 스타"로 발음됨) 는 그래프 순회와 경로 찾기를 위해 사용되는 알고리즘으로, 그 완결성, 적합성, 그리고 최적 효율 덕분에 컴퓨터 과학 분야에서 종종 사용된다¹.

 한마디로 경로 탐색 알고리즘의 하나 입니다. 

---

알아야할 공식 하나

겁먹지 않도록 합시다. 알고보면 별거 없습니다.

 

$f(n) = g(n) + h(n)$

$f(n): 최소화 하고자 하는 값$

$g(n): 시작노드에서 현재 노드까지 Cost(여기선 거리)$

$h(n): 현재 노드에서 도착점까지 직선거리(이 경우에만 해당됨) $

 

$h(n)$은 $Heuristic$(경험적인)의 약자입니다. 우리는 유럽의 도시들의 거리에 대해서 하고있는데, 경험적으로 우리는 한 지점에서 다른지점까지 가장 짧은 거리가 직선까지라는 것을 알고있으니, 우리가 다루는 경우에선 직선거리라고 생각하면 됩니다. 다른 분야에서 쓰일때는 그에 맞는 $h(n)$ 값을 찾아야 합니다.

---

그림으로 바로이해

그림으로 이해하자. 알고리즘적 사고는 위키피디아에 있음.

 알고리즘 식으로 표현하면 코딩에 활용할 수 있으며 논리적이지만, 직관적이지 못한면이 있습니다. 우리의 목표는 알고리즘을 직접 코드로 구현하는게 아닌, 원리를 이해한뒤 Neo4j에서 활용하는 것이니 그림을 통해 이해해보도록 하겠습니다.

이 그림만 이해할 수 있으면, 최소한의 원리는 이해한 것입니다.

---

기본 구조 이해

위 움짤을 한스탭씩 따라가보자.

기본적인 노드와 엣지의 구조

시작점, 도착점, 지나온점, h(n), g(n)이 있습니다.

 노드를 표현한 부분에선 3가지를 보시면 됩니다. 시작점, 끝점, 그리고 지나온 점. 위의 움짤을 보면 이 3가지를 중심으로 그림이 획획 하고 바뀌는 것을 알 수 있습니다. $h(n)$은 해당하는 노드와 도착점 사이의 직선 거리입니다.

---

각 $h(n)$ 표시

모든 노드와 도착점 사이의 직선거리

01234

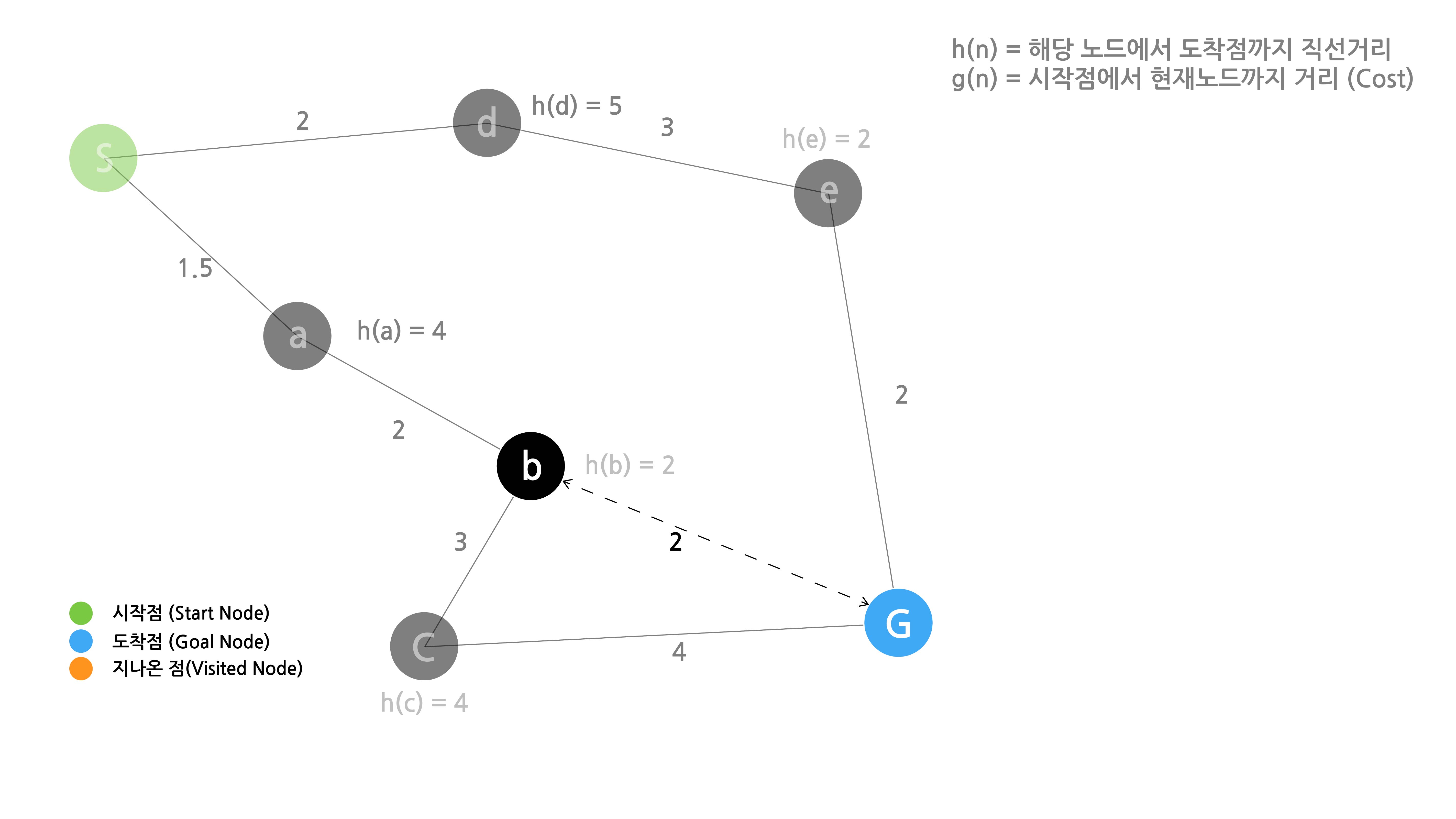
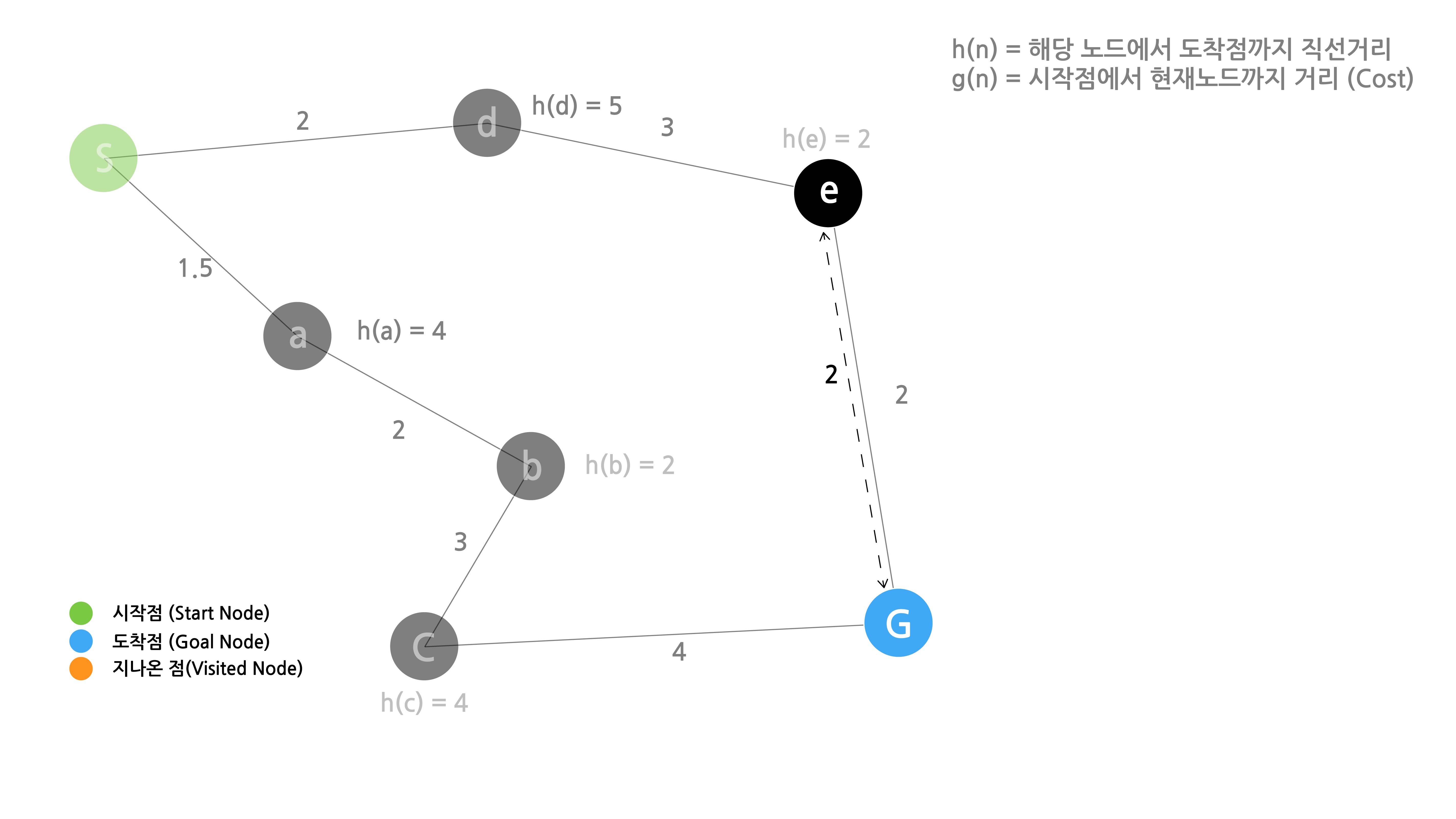
위의 그림에서 모든 직선 거리를 표시했습니다. 그럼 본격적으로 시작해보도록 하겠습니다.

---

단계별 진행 

인접 노드들의 $f(n)$ 계산 -> 비교 -> $f(n)$이 작은쪽을 노드를 선택, 큰쪽은 Hold -> 선택된 노드의 인접 노드들의 $f(n)$ 계산 -> ... -> 선택된노드 == 도착점인 경우 멈춤

 알고리즘을 잘 아시는 분들은 아셨겠지만, 재귀 알고리즘(Recursive Algorithm)인 것을 볼 수 있습니다. 기준점으로 부터, 인접한 노드들의 $f(n)$ 값을 구하고, 이들을 비교합니다. 그 후 $f(n)$ 값이 작은쪽을 다음 노드로 선택하고, 큰쪽은 Hold 즉, 어딘가에 저장해 놓습니다. 다시 선택된 노드의 인접노드의 $f(n)$값을 구합니다. 이때부터 약간 달라지는데, 인접 노드에서 구해진 $f(n)$ 값만 비교하는게 Hold해놓은 값도 비교합니다. 만약 Hold 한쪽의 $f(n)$값이 작다면, 이 노드가 선택되며, 계산한 나머지 $f(n)$값과 노드들은 Hold 합니다. 

---

결론부터 보여주자면...

바쁘신 분들은 아래 슬라이드를 돌려보시면 됩니다.

012345

결론 부터 이야기하는 두괄식 설명

---

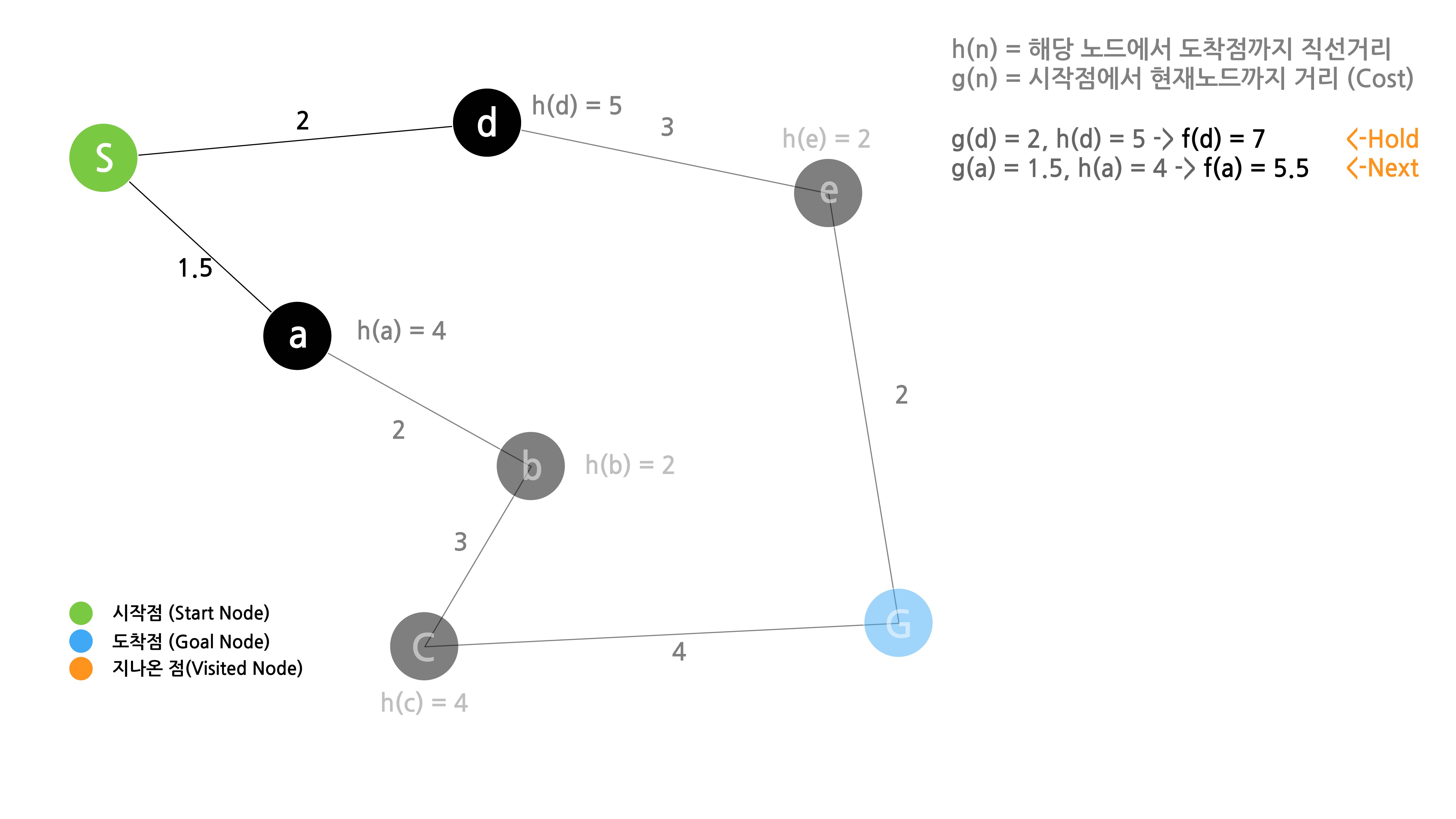
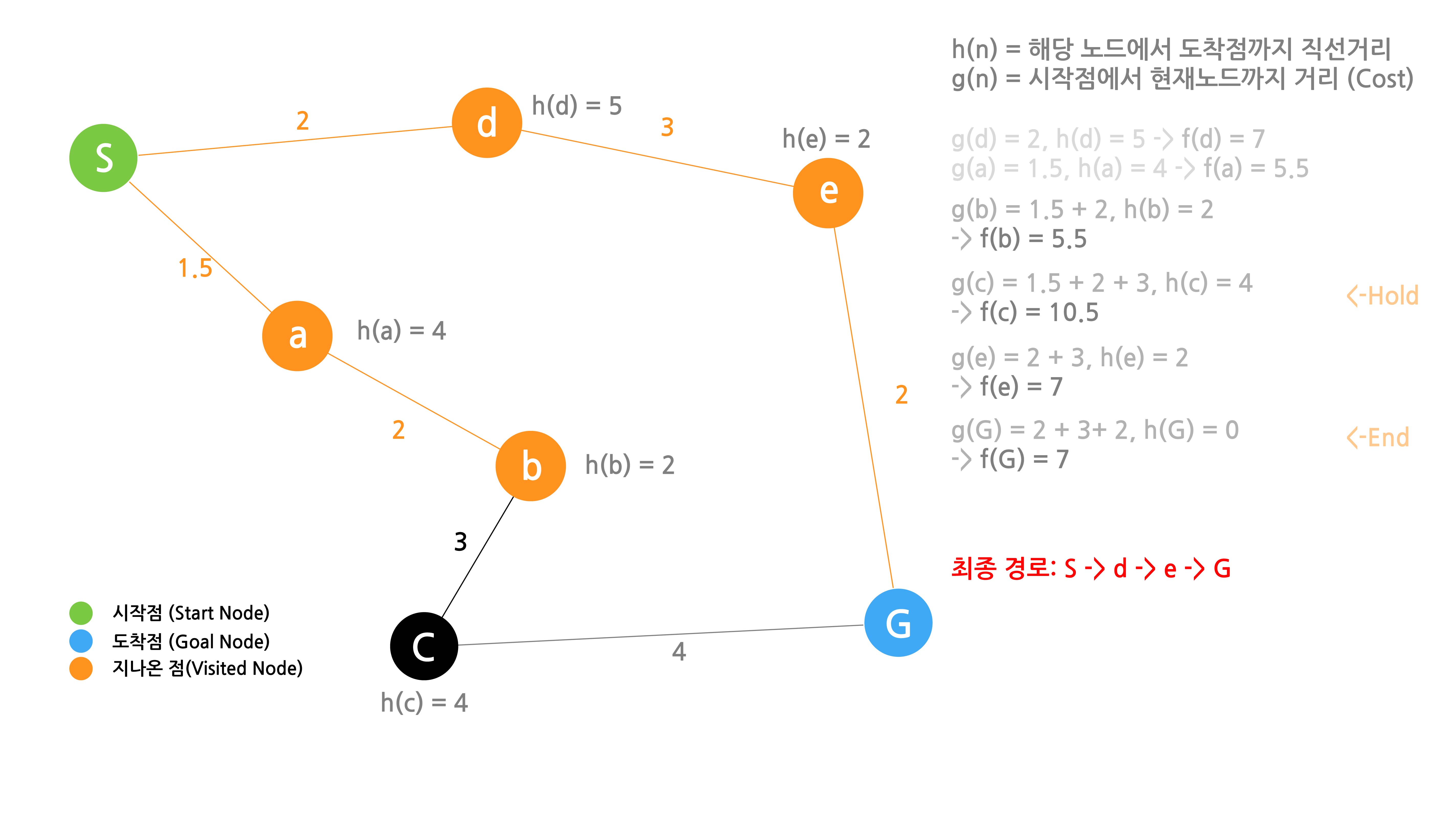
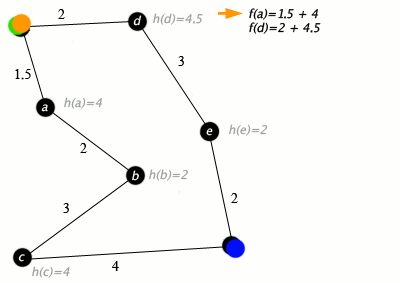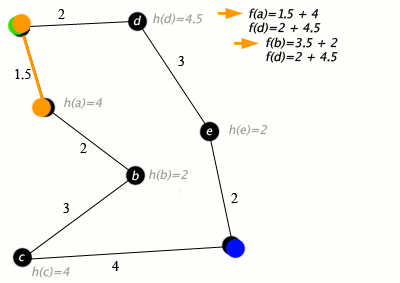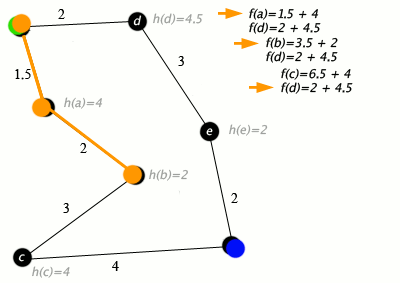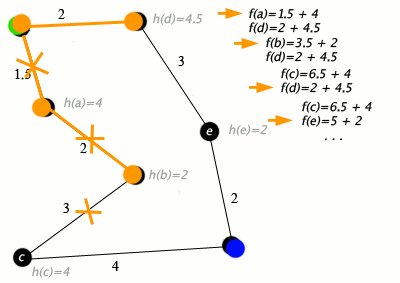
1. 시작점의 인접노드의 $f(n)$구하여 비교하고 다음노드 선택하기

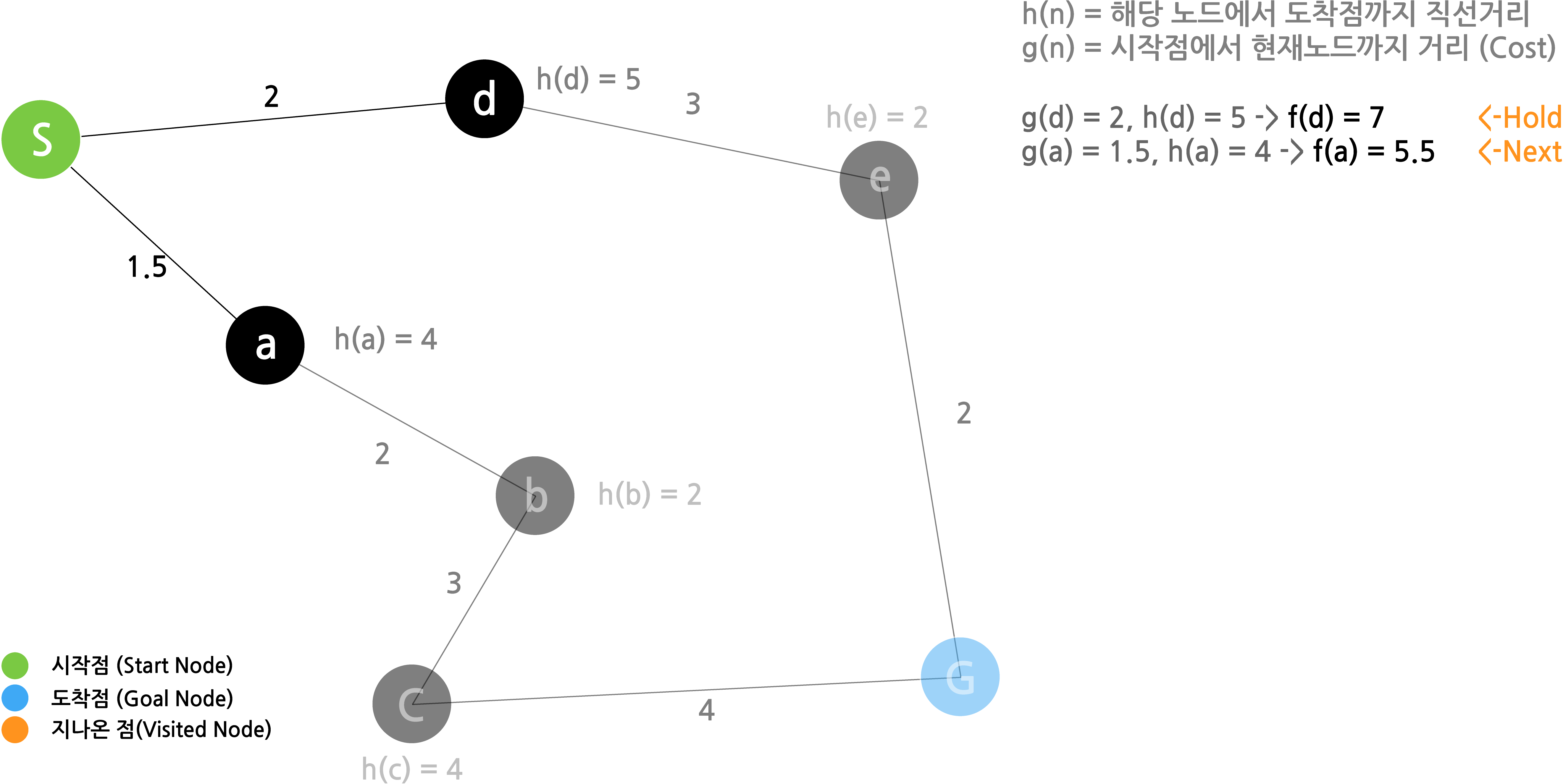
 다음노드를 선택하기 전에 $f(n)$ 값을 구합니다. 

 $f(d)$를 보면 d 까지 이동하기 위한 cost는 2이며 따라서 $g(d)=2$가 성립합니다. $h(d)$는 이미 계산되어 주어진 5 입니다. 두 값을 더하면 $f(d)=7$ 입니다.

 $f(a)$ 값도 마찬가지 입니다. $cost = 1.5 -> g(d) = 1.5$이며 $h(a) =4$ 입니다. 따라서 $f(a)=5.5$입니다. 

두 값을 비교하여 $f(a)$가 작기때문에 a가 다음 노드로 선택됩니다.

---

 

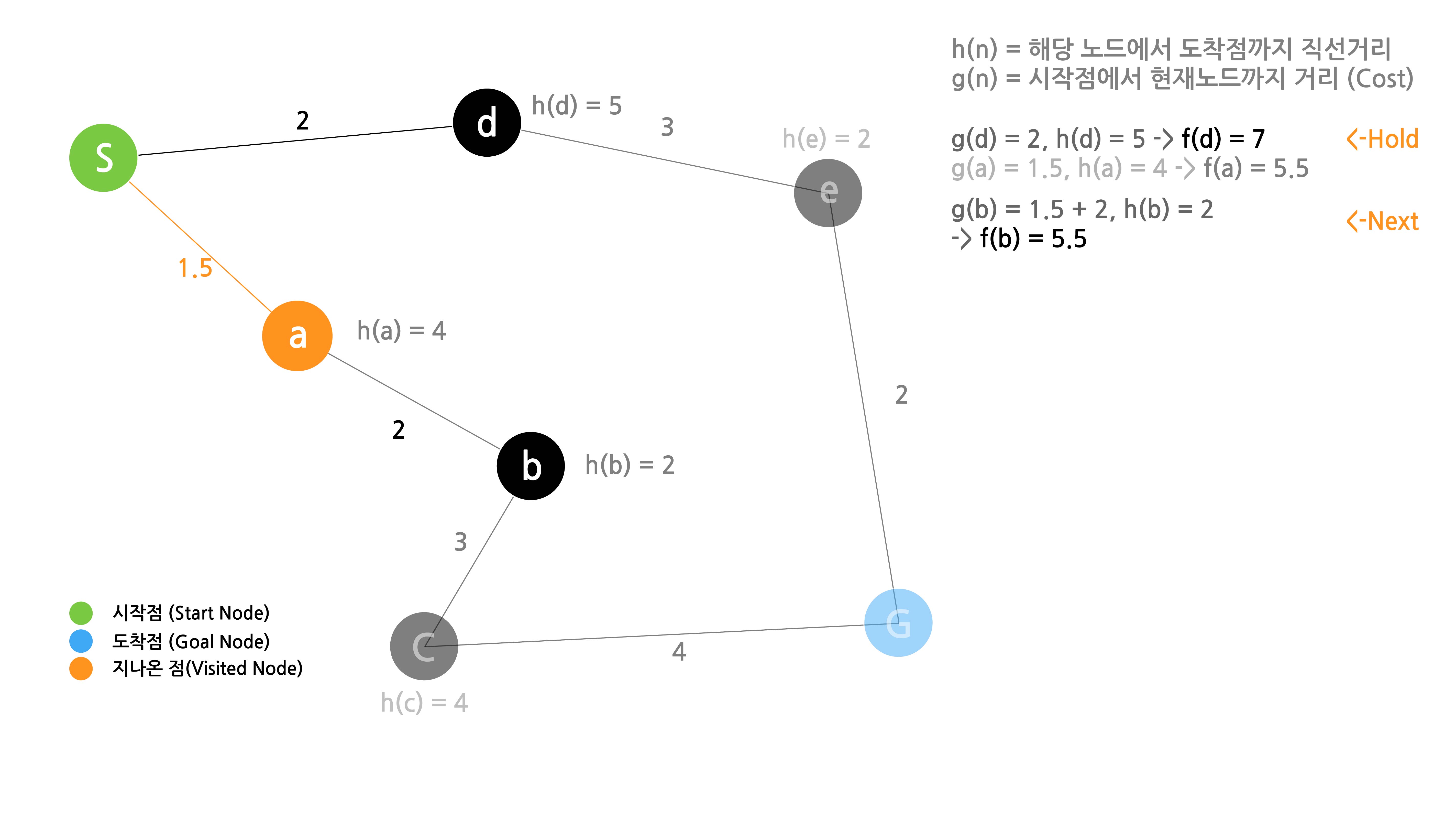
2. a의 인접노드(b)의 $f(b)$값 구하기

a의 인접노드가 b 한개인 관계로 하나만 구하면 됩니다.

f(b)값을 구하고 f(d)값과 비교합니다.

기호 말고 변화가 없어서 조금 당황스럽긴 하지만, $f(b)$값을 구했습니다. 값은 $f(a)$와 동일한 5.5입니다. 여기서 부터 중요한데, 이 구해진 값을 우리가 Hold 해놓았던 $f(d)$값과 비교합니다. 지금 이 예제에선 hold된 값이 하나밖에 없지만, hold된 값이 여러개라면, 모든 hold된 값들과 비교해야 합니다.

 이 경우에도 $f(b)$가 더 작기 때문에 b노드를 선택합니다.

---

3. b의 인접노드(c)의 $f(c)$값 구하기

앞과 과정은 동일합니다. 

이제 선택된 노드가 d 인것을 볼 수 있다.

앞과 계산 과정은 동일하기 때문에 넘어가도록 하겠습니다. $f(c) = 10.5$ 가 나왔습니다. 여기서 반전이 일어나는데, 이제 더이상 S->a->b 경로로 이동하지 않게 됩니다. 왜냐하면

$f(c)=10.5, f(d) =7$

$∴f(d)<f(c)$

이기 때문입니다. 이제는 d방향으로 길을 틀게 됩니다.

---

4. 앞의 과정 반복하기

끝날때까지 계속 반복하겠습니다.

인접 노드 e에 대해서 계산 후, 홀드된 c와 비교

 d의 인접노드인 e의 $f(e)$ 값을 구하고 $f(c)$와 비교합니다. 여기서 공식

$f(e) < f(c)$

가 성립하기 때문에, e가 다음 경로가 됩니다.

---

5.e의 인접 G. 즉, 마지막

G에 도달함으로 끝나게 됩니다.

$f(G)$ 값을 구합니다. 여기서도 마찬가지로 비교를 통해

$f(G) < f(c)$

가 성립합니다. 따라서 최종 경로는 S -> d -> e -> G 가 됩니다.

 

6.최종경로

 이러한 과정을 거쳐 A* 알고리즘의 작동원리를 알아봤습니다. 아래는 위키피디아에 있던 그림들인데, 이들을 보며 다시한번 생각해 봅시다.

---

다른 그림들로 복습해보기

잘 보면, 어떤 루트들은 계속 진행되는데, 어떤 루트들은 멈춘것을 볼 수 있음. 즉 Hold 와 Next의 관계가 있는 것.

처음 시작을 보면, 대각선 방향으로 움직이다가 장애물을 피해 움직이는 것을 볼 수 있음.

---

더 생각해보기

아래 그림에서 h(e) =2 이며 이는 e와 G 사이의 코스트와 같은데 항상 그러한가?

노드 c와 e를 보면 g와의 cost값이 h(n)과 동일한 것을 볼 수 있다.

 저는 마지막 직전 노드들의 h(n) 값이 마지막노드와 항상 일치하느냐 라고 묻는다면, 당연하다고 답하겠습니다. 이유는 다음 그림과 같습니다.

이런 길의 시작점 부터 끝점까지 직선거리는 분명히 도로의 길이와는 다르다.

 위와같은 도로 사정을 가진다면 당연히  $f(n) \neq cost$ 의 조건이 될 것입니다.

---

참고자료

---

유투브 강의

위키피디아

---

풋노트

---

1. 위키피디아 ↩︎